座標とベクトル

座標系

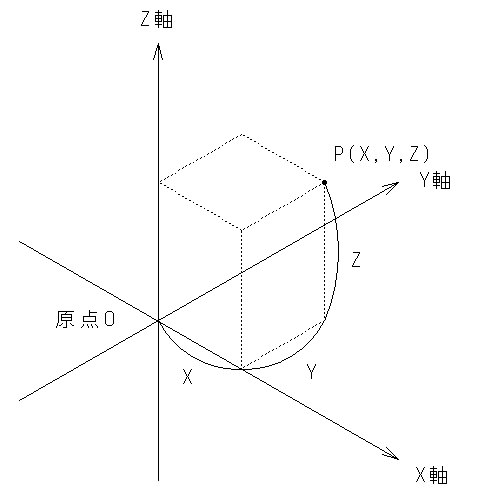
物体の運動は空間の中で行われ、運動している間に時間が経過する。この物体の存在している空間は、古典力学ではユークリッド幾何学によって定義される、３次元ユークリッド空間が使用される。この空間では直交座標系、またはデカルト座標系と呼ばれる座標系を使用する。直交座標系とは、原点Oを通り互いに直交する３本の直線を基準として表わされる座標系である。この３本の直線は座標軸と呼ばれ、それぞれx軸、y軸、z軸と呼ばれる。

任意の点Pの位置は、点Pから各軸へ下ろした垂線を読み、(x,y,z)で一意的に表わされる。x,y,zはそれぞれ、x,y,z座標成分、またはx,y,z成分と呼ばれる。

ベクトル

点Pの位置は、x,y,zの３つの座標を用いる他に、原点Oから点Pへ引いた矢印によって表すこともできる。この矢印をベクトルと呼ぶ。原点Oから点Pへのベクトルであるため、ベクトル $\vec{OP}$ で表わされる。ベクトルは、２つのベクトルが異なる位置にあっても、同じ大きさと同じ方向を持っていれば、同一のベクトルとして扱われる。

また、原点Oを始点とするベクトルを特に位置ベクトルと呼ぶ。位置ベクトルも通常のベクトルと同じく $\vec{OP}$ と書かれることもあるが、一般的にはrで表わされる。位置ベクトルはその成分を縦に書き並べて

r = (\begin{matrix} x \\ y \\ z \end{matrix})

と表すこともできる。

x,y,z軸に沿って単位長さのベクトルを考え、これらをそれぞれ i , j , k とすると、位置ベクトルrは

r = x i + y j + z k

で表わされる。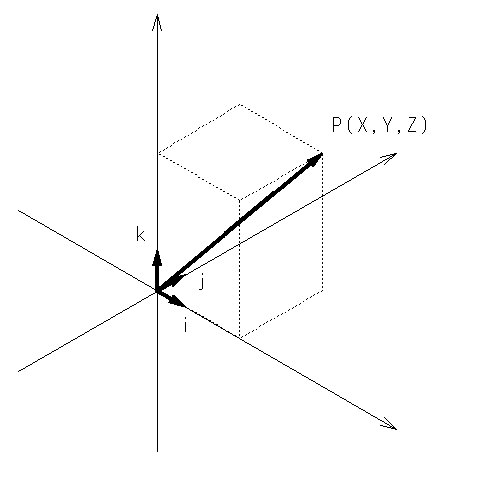

原点Oから点P(x,y,z)までの距離はピタゴラスの定理により $\sqrt{x^{2} + y^{2} + z^{2}}$ となるので、

| r | = \sqrt{x^{2} + y^{2} + z^{2}} = r

と書かれ、これをベクトルrの絶対値という。

ベクトルは大きさの他に方向を持っているが、長さや質量などのように、大きさのみを表す量はスカラーと呼ばれる。一般に3次元空間では、スカラーは3⁰=1個の成分を持ち、ベクトルは3¹=3個の成分を持つ。この他に3²個、3³個…の成分を持った量が考えられ、それぞれ２階、３階…のテンソルと呼ばれる。