予算制約線と最適消費点

多くの人は、好きなものを好きなだけ消費しているわけではない。支出は所得によって制限されるため、限られた予算の中で最も満足度が高くなる組み合わせを選ぶことになる。

予算制約線

仮に、毎月一万円で2つの財を消費できるとする。そして第1財の単価は千円、第2財は五百円とした場合、一万円をすべて第1財に振り分けると10購入でき、すべて第2財に振り分けると20購入できる。これをグラフ化して、両極端の点を線で結ぶと以下のようになる。

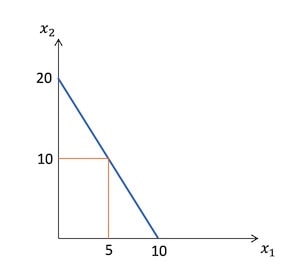
この青線は予算制約線と呼ばれ、これは消費者が購入できる消費の組み合わせを示している。予算をすべて消費に回した場合は、予算制約線上のどこかの点に位置することになる。

ある消費者の所得を $I$ 、財の価格を $p$ 、財の消費量を $x$ として、所得をすべて消費に回した場合は、

p x = I

と書ける。この式は予算制約式と呼ばれる。

簡単化のために財が2つしかないケースを考え、第1財と第2財の価格をそれぞれ $p_{1}$ , $p_{2}$ 、第1財と第2財の消費量をそれぞれ $x_{1}$ , $x_{2}$ とすると、

p_{1} x_{1} + p_{2} x_{2} = I

となる。

この式を変形すると、

x_{2} = - \frac{p_{1}}{p_{2}} x_{1} + \frac{I}{p_{2}}

となる。この式が「

y = a x + b

」の形になっていることからもわかるように、予算制約線の傾きは

\frac{p 1}{p 2}

、つまり価格の比率になる。

予算制約線は固定でさまざまな無差別曲線を描くと、そのパターンは「交点が2つ」「交点（接点）が1つ」「交点なし」が考えられる。

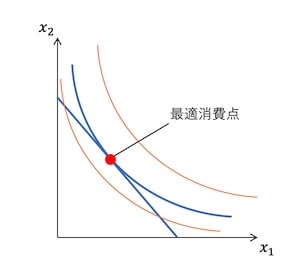
図のように「交点なし」で予算制約線を越えているものはそもそも購入ができない。「交点が2つ」かあるいは予算制約線よりも左下にくる無差別曲線は、効用を改善できる余地があるので最適消費ではない。

消費者にとって効用を最大化する最適な消費の組み合わせは、予算制約線と無差別曲線が接する点となる。この点は最適消費点と呼ばれる。

この最適消費点での限界代替率は、予算制約線の傾きと一致する。つまり、最適消費点における限界代替率は、 $\frac{p 1}{p 2}$ になることがわかる。

参考書籍（PR）