短期の利潤最大化

完全競争

生産要素のうち労働投入量だけを変えることができ、生産物の価格や賃金が変化しない完全競争の場合の利潤最大化を見ていく。

ちなみに、個々の生産者や消費者が市場価格を一定として見ることは、市場価格をそのまま受け入れるということからプライステイカーの仮定と呼ばれる。完全競争とは、すべての生産者や消費者がプライステイカーであることである。

価格を $p$ 、賃金を $w$ とし、労働を $L$ 、生産量を $y$ とすると生産関数は $y = f (L)$ と書ける。利潤を $π$ とすれば、

π = p f (L) - w L

となる。

価格 $p$ と賃金 $w$ は固定で、変化するのは労働 $L$ だけなので、労働量をいくつにすれば利潤を最大化できるのかを見ていくことになる。

$y = f (L)$ なので、先程の式の生産関数を生産量 $y$ にすると、

π = p y - w L

となり、変形すると

y = \frac{w}{p} L + \frac{π}{p}

と、直線の式になる。このとき、利潤を固定（切片を固定）したときに描かれる直線は等利潤線と呼ばれる。また、この直線の傾きである

w

p

は実質賃金率と呼ばれる。

生産関数と等利潤線をグラフにすると以下のようになり、その接点が利潤最大点となる。

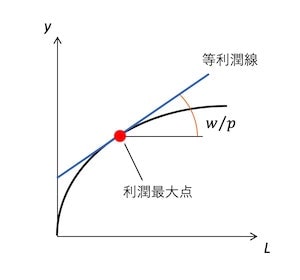
生産関数の接線が等利潤線になるということは、等利潤線の傾き $w$ / $p$ と労働の限界生産性 $f' (L)$ は一致することになる。つまり、

f' (L) = \frac{w}{p}

が、利潤最大化条件となる。

この式の両辺にpをかけると、

p f' (L) = w

となる。左辺は労働の限界生産物の価値と呼ばれる。右辺は労働

L

を限界的に1単位増やしたときに増加する賃金である。左辺の方が大きい場合は労働を増やせば利潤を上げることができ、右辺の方が大きい場合は労働を減らせば利潤は上がる。

参考書籍（PR）