限界効用

財の限界効用とは、財を1単位多く消費したときに得られる効用の変化を表している。

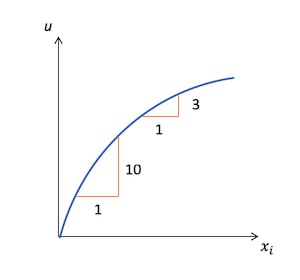
経済学では、1つの財の消費量が増えるほど効用も増えることを仮定しているのと同時に、ほとんどの財において消費量が増えれば増えるほど効用の増加率が小さくなる、つまり限界効用が低下することを仮定している。これを限界効用逓減の法則という。横軸を財の消費量、縦軸を効用とすると以下のようになる。

数式による表現

限界効用は、消費量を微調整したときの効用の変化ともいえるので、効用を消費量で微分することによって得られる。

効用を $u$ 、第 $i$ 番目の財の消費量を $x_{i}$ とした場合、第 $i$ 財の限界効用は Marginal Utility の頭文字をとって ${MU}_{i}$ と表せる。そして第 $i$ 財の消費量 $x_{i}$ だけを微分すると

{MU}_{i} = \frac{\partial u}{\partial x_{i}}

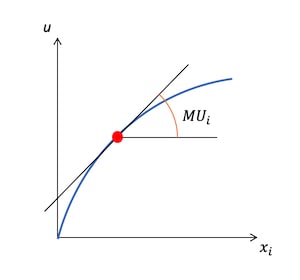
となる。これを偏微分といい、この場合、第

i

財の消費量

x_{i}

だけを変化させ、それ以外の財の消費量は変化させずに定数として扱うものである。「

\partial

」は「ラウンド・ディー」と読む。

これをグラフで表すと、限界効用とは接線の傾きであることがわかる。

財の限界効用を、財を1単位多く消費したときに得られる効用の変化として捉えると、下図のようになる。ある財の消費量 $x_{i}$ の変化量を $Δ x_{i}$ 、そのときの効用の変化量を $Δ u$ としている。

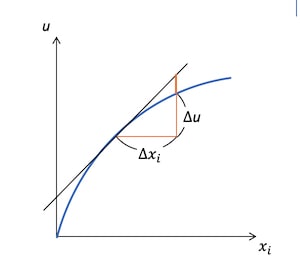
つまり、効用の変化量は限界効用と財の消費量の積で得られるため、

Δ u = \frac{\partial u}{\partial x_{i}} Δ x_{i}

と書ける。

ただし、上図を見ても分かる通り、接線と曲線の間にはすき間があるため、厳密にはこの等式は成り立たない。微分したときの限界効用というのは、消費量を「限界的に」1単位増やしたときの効用の変化なので、消費量の変化 $Δ x_{i}$ が十分に小さいという条件が必要になる。それを表したのが以下の式となる。

d u = \frac{\partial u}{\partial x_{i}} d x_{i}

全体の効用はそれぞれの財を消費することによる効用の和となるので、財が全部で $N$ 個あるとすると、

d u = \frac{\partial u}{\partial x_{1}} d x_{1} + \frac{\partial u}{\partial x_{2}} d x_{2} + \dots + \frac{\partial u}{\partial x_{N}} d x_{N}

と書ける。

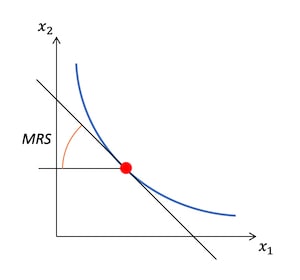
「無差別曲線と限界代替率」のページでは、限界代替率を「第1財の消費量を1単位増やすのに、第2財をどれだけ支払えば効用を維持できるか」と書いて、以下の図で示した。

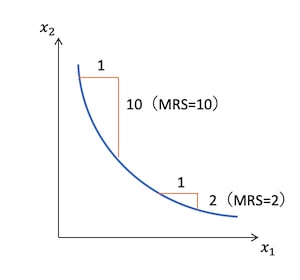
これも限界効用と同じように、微分を用いた数式で表すと以下の図のように、無差別曲線の接線の傾きとして表せる。

2つの財の消費量を変化させたときの全体の効用の変化は、それぞれの財における効用の変化の和となるので、上で示した式から、

d u = \frac{\partial u}{\partial x_{1}} d x_{1} + \frac{\partial u}{\partial x_{2}} d x_{2}

と書ける。無差別曲線は効用が一定になる点を結んだもので、全体の効用が変化しないということなので

0 = \frac{\partial u}{\partial x_{1}} d x_{1} + \frac{\partial u}{\partial x_{2}} d x_{2}

となる。

これを変形すると

\frac{d x_{2}}{d x_{1}} = - \frac{\partial u / \partial x_{1}}{\partial u / \partial x_{2}}

となる。

これは無差別曲線の傾きであり、符号がマイナスになるのでプラスに変えたものが限界代替率になる。右辺を見るとわかるように、限界効用の比にもなっている。

参考書籍（PR）