補償需要関数と支出関数

一定の効用を達成するために、費用を最小化する消費計画である補償需要関数と、ある価格の下で一定の効用を達成するために、最低限必要な金額である支出関数を見ていく。

補償需要関数

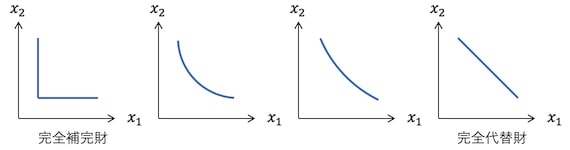
「無差別曲線と限界代替率」のページでは、無差別曲線の2つの極端な例は完全代替財と完全補完財であり、完全代替財の無差別曲線は右下がりの直線となり、完全補完財のものはL字型になることを見た。多くの財はこの2つの間に位置することになるが、それは無差別曲線の形が直線とL字型の中間になることを意味する。つまり、完全ではないものの、代替財と補完財に分けられるはずである。

価格と効用が一定で、支出を最小化する組み合わせを求めるものは支出最小化問題と呼ばれ、その解は補償需要と呼ばれる。補償需要を $h$ とすると、補償需要 $h$ は価格 $p$ と効用 $u$ の関数になるので、 $h (p, u)$ と書ける。

この補償需要関数 $h (p, u)$ が価格の変化に対してどのように反応するかで、無差別曲線の曲がり具合、すなわち代替性と補完性の程度を知ることができる。価格が限界的に1単位変化したときの補償需要の変化は

\frac{\partial h_{i}}{\partial p_{j}}

となる。

以下の図を見てもわかるように、補完性が強い場合、価格の変化に対して補償需要はあまり変化しないが、代替性が強いときは、価格の変化に対して補償需要は大きく動く。

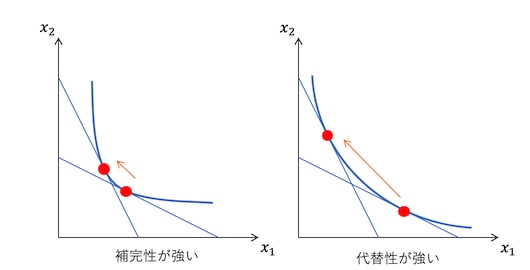
自己代替効果

ある財の価格が上昇するとその財の補償需要は増加しない、つまり減少するか変わらないかなので

\frac{\partial h_{i}}{\partial p_{i}} \leq 0

となる。これは「自己代替効果は非正である」という。

通常は自己代替効果はマイナスになる、つまり $\frac{\partial h_{i}}{\partial p_{i}} < 0$ となり、このとき補償需要関数を $h (p, u)$ とすると、

\frac{\partial h_{j}}{\partial p_{i}} < 0

　なら第

i

財と第

j

財は補完財

\frac{\partial h_{j}}{\partial p_{i}} > 0

　なら第

i

財と第

j

財は代替財

となる。

支出関数

補償需要関数 $h (p, u)$ が、一定の価格と効用で支出を最小化する消費量の組み合わせを求める関数なわけだから、これに価格 $p = (p_{1}, p_{2}, \dots, p_{N})$ をかければ、効用 $u$ を達成するために最低限必要な金額が求められる。

これは

e (p, u) = p h (p, u)

と書いて、支出関数と呼ばれる。

シェファードの補題

支出関数を第 $i$ 財の価格で微分すると

\frac{\partial e (p, u)}{\partial p_{i}} = h_{i} (p, u)

となる。これはシェファードの補題と呼ばれる。

双対性

効用 $u$ と価格 $p$ が一定で、支出を最小化する消費量の組み合わせを求めるアプローチ（ $h (p, u)$ ）と、所得 $I$ と価格 $p$ が一定で、効用を最大化する消費量の組み合わせを求めるアプローチ（ $x (p, I)$ ）は、どちらも同じ最適消費点を求める方法である。このように、最適消費が支出最小化問題の解と見ることもできるし、効用最大化問題の解と見ることもできることを双対性という。つまり

h (p, u) = x (p, I)

ということである。

参考書籍（PR）