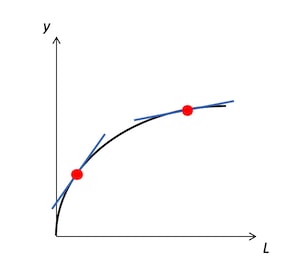
生産要素と生産関数
企業の規模や活動形態、生産工程などはさまざまであるが、伝統的なミクロ経済学の理論である価格理論では、生産要素を投入し生産物を産出する変換システムとして捉え、企業の内部で起こることにはブラックボックス化される。
生産要素
生産要素とは財・サービスの生産に必要な投入物であり、最も重要なものとして「労働」「資本」「土地」の3つがある。労働は、技術力や生産力を持つ労働者あるいは労働者の時間である。資本は、オフィスや工場、機械などの固定的な生産設備ことで、多期間にわたって生産に使える財をさす。土地は、生産過程で使用される物理的な空間である「土地」を指す。土地については議論がややこしくなるので、ここでは扱わない。
生産関数と生産可能性集合
生産要素には原材料なども含まれるが、簡単化のために、まずは「労働」だけを変化させて生産物を作り出す場合、つまり労働以外を定数とする場合を考えてみる。
労働を、生産物をとした場合、関数と書ける。この関数を生産関数という。これは、労働の投入量によって生産物の産出量が変化するという単純なものである。
労働を横軸、生産物を縦軸としてグラフ化すると、以下の図のようになる。
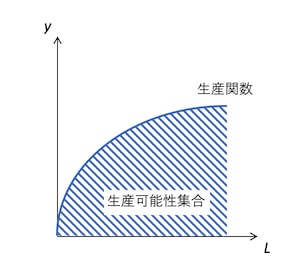
この図の斜線部は、その企業が達成できる投入量と産出量の可能な組み合わせを表しており、生産可能性集合と呼ばれる。生産関数は、それぞれの投入量で最も高い産出量を表す点の集合として捉えることができる。
ミクロ経済学における短期と長期
ミクロ経済学では、固定された生産要素が存在せずすべての生産要素の量を変えることができる期間を長期といい、一部の生産要素の量が固定される期間を短期と呼んでいる。
一般的に見ると、一日あたりの労働時間を変化させることは比較的容易であるが、建物や機械などの設備の数を一日毎に変化させることは難しい。
上述した生産関数は、労働以外の生産要素の量を固定化しているため、短期の生産関数として見ることができる。ただし、現実的ではないが、生産要素が労働しかない場合は長期の生産関数とも言える。
一方で、すべての生産要素が労働と資本の2つの場合、この2つを変数とする生産関数は長期の生産関数と呼ばれることもある。資本をとした場合、関数と書かれる。
労働の限界生産性
労働だけを変数とする短期の生産関数は、どれだけの労働量を投入すればどれだけの生産物を産出できるのかを考えるのに役に立つ。「限界効用」のページでも見たように、限界原理に基づいて数式化すると分析しやすくなる。
労働を限界的に1単位増やしたときの産出量の変化は、生産関数を労働で微分することによって求められる。つまり、、あるいはで表される。これを労働の限界生産性という。
通常は、労働量が少ないときは労働の限界生産性は高いが、労働量を増やしていくと労働の限界生産性は低下していく。つまり、労働量を増やせば増やすほど、労働を1単位増やしたときの生産量の増加分が小さくなる。これを、限界生産性逓減の法則という。