さまざまな費用と供給曲線

費用のさまざまな尺度と、供給曲線や生産者余剰、企業の利潤について見ていく。

総費用曲線

ある生産物を作るのに、全体として必要になる費用は総費用と呼ばれる。

「生産要素と生産関数」のページでも見たように、労働を増やし続けていくと生産量の増加率は低下していく（限界生産性逓減の法則）。これは、生産量が多くなると、生産量を1単位増やすのにより多くの労働量、つまりより多くのコストが必要になるということでもある。

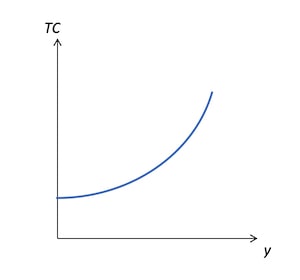
横軸を生産物 $y$ 、縦軸を総費用 $TC$ （Total Cost）としてグラフにすると以下のようになり、これは総費用曲線と呼ばれる。

可変費用と固定費用

総費用は、大きさを自由に変えられる生産要素にかかる可変費用と、固定的な生産要素にかかる固定費用に分けることができる。

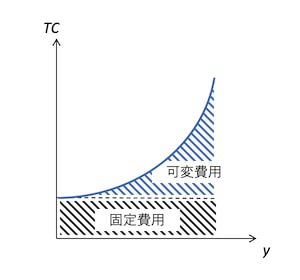
上の総費用曲線の図を見てもわかるように、生産量をゼロにしても費用はゼロにならない。この生産量をゼロにしても支払わなければならない費用が固定費用であり、生産量を変えても変化しない。逆に生産量によって変化する部分が可変費用である。

すべての生産要素の大きさを変えられる長期においては、費用はすべて可変費用となる。

固定費用のうち、売却や処分などによって回収することができない費用はサンク・コスト（埋没費用）と呼ばれる。固定費用は、このサンクされた固定費用とサンクされていない固定費用に分けられるが、このページでは固定費用はすべてサンク・コストとして扱う。

平均費用と限界費用

生産物 $y$ の1単位あたりの費用は、総費用 $TC$ を生産物 $y$ で割ると得られる。これは平均費用と呼ばれ $AC$ （Average Cost）と書かれる。

一方、生産物を限界的に1単位増やすのに必要な費用は限界費用と呼ばれ $MC$ （Marginal Cost）と書かれる。総費用関数を $C (y)$ とすると、限界費用は、総費用関数を生産量で微分する $C' (y)$ となる。

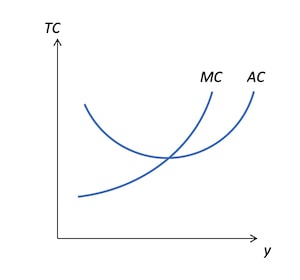
総費用曲線に基づいて生産量を増やしていくと、平均費用と限界費用が一致する点があることがわかる。平均費用はこの点で最も小さくなり、その点から離れるほど平均費用は増加していく。

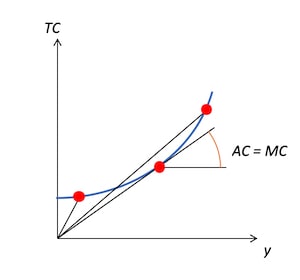
つまり、平均費用をグラフにするとU字型になり、限界費用との関係は以下のグラフのようになる。

供給曲線

費用と生産量の関係において、生産者にとって最も合理的な選択は利潤を最大化することで、利潤は売上から費用を差し引いたものである。売上は生産物の価格 $p$ と生産量 $y$ をかけたものなので $p y$ 、費用を総費用関数 $C (y)$ とすれば、利潤は $p y - C (y)$ と書ける。このとき、利潤を最大化する生産量 $y$ を求めることは利潤最大化問題と呼ばれる。

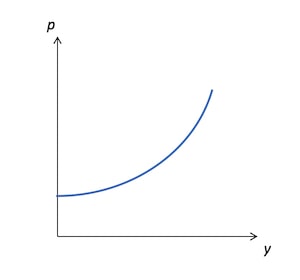
生産量とは供給量のことでもあり、利潤を最大化する供給量は価格 $p$ に依存するため、供給関数（Supply Function）は $S (p)$ と書ける。横軸を生産量 $y$ 、縦軸を価格 $p$ として、供給関数をグラフにしたものが以下の図であり、これは供給曲線と呼ばれる。

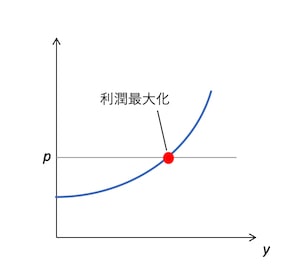
限界費用を描いた図を見ると、生産物の価格 $p$ が固定である完全競争の場合、限界費用が価格よりも小さいときは、生産量を増やせば費用の上昇よりも売上の上昇が大きくなるので利潤を増やすことができる。逆に限界費用が価格よりも大きいときは、生産量を減らせば売上の減少よりも費用の減少が大きくなるので利潤を増やすことができる。つまり、利潤を最大化する生産量（供給量）は、価格が限界費用に等しくなるときであることがわかる。こうした標準的なケースにおいては供給曲線と限界費用曲線は一致するということである。

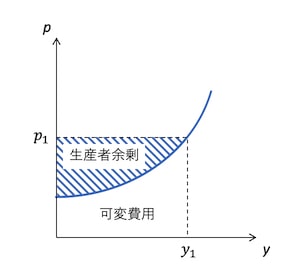
生産者余剰と利潤

売上は生産物の価格と生産量をかけたものなので、以下の図の価格 $p_{1}$ と生産量 $y_{1}$ での売上は、四角形の面積になる。供給曲線は限界費用曲線でもあるので、供給曲線の下側の部分は生産量 $y_{1}$ を産出するための可変費用である。したがって、供給曲線の上側の部分は、売上から可変費用を差し引いたものになる。この、売上から可変費用を差し引いたものは生産者余剰と呼ばれる。生産者余剰から固定費用を差し引いたものが利潤となる。

参考書籍（PR）