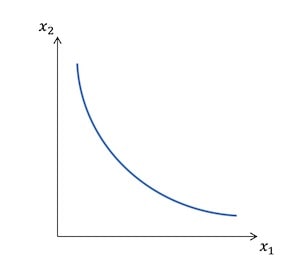
無差別曲線と限界代替率
社会に個の財・サービスがあるとして、ある消費者の第番目の財の消費量をとすると、その消費者の消費パターンは、
で表される。これはその消費者の消費計画と呼ばれる。同じ効用を与える消費計画は無数にあり、財が3つ以上の場合は分析するのも直感的に理解するのも難しくなる。そこで財が2つの場合を考えて、横軸と縦軸をそれぞれの財の消費量として同じ効用を与える点を結ぶと、その形は通常は曲線になる。「同じ効用を与える」というのは「無差別である」ということなので、このときの曲線は無差別曲線と呼ばれる。
無差別曲線の4つの性質
ほとんどの無差別曲線には以下の4つの性質がある。
- 右上にあるほど効用が高い
- 右下がりである
- 互いに交わらない
- 原点に向かって凸である
1の「右上にあるほど効用が高い」というのは、消費量の多いほうが好ましいということである。
2の「右下がりである」というのは、2つの財が代替可能であることを示している。一方の財の消費量を増やした場合、もう一方の財の消費量を減らしたとしても、同じ効用を維持することができる。逆に一方の財の消費量を減らした場合は、もう一方の財の消費量を増やさなければ、同じ効用を維持することができないということでもある。
3の「互いに交わらない」というのは、もし交わってしまうと、1の「消費量の多いほうが好ましい」ということに反する。別の見方をすると、同じ効用を与える点を結ぶと1本の無差別曲線になるが、これよりも高い効用の無差別曲線を描いても1本の曲線、つまり合計2本の曲線になる。これが交わってしまうということは交点が同じ効用になることを意味するので、別々の効用の無差別曲線を描いていることと矛盾する。
4の「原点に向かって凸である」というのは、限界代替率が逓減することを示している。限界代替率については以下に記述する。
限界代替率
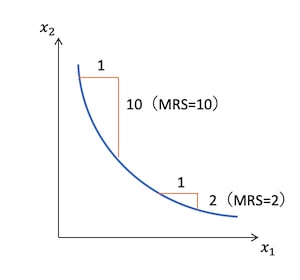
無差別曲線は、2つの財を交換しても効用が同じになる点を結んだものである。これは、無差別曲線上のどの点の傾きをとっても、一方の財をもう一方の財と交換してもよいと思う比率に等しいことを意味している。この比率のことを限界代替率(Marginal Rate of Substitution)といい、頭文字をとって「MRS」と表す。また、「第1財の第2財に対する限界代替率」というときには「MRS12」と表したりする。これは、第1財の消費量を1単位増やすのに、第2財をどれだけ支払えば効用を維持できるかを示している。
多くの財について、無差別曲線が原点に向かって凸になる理由は、第1財の消費量を増やしていくと、その第1財の消費量を1単位増やしたときに第2財を支払う量が小さくなっていくためである。つまり、限界代替率が低下していくということである。これは2つの財を比較したときにその消費者にとって、第1財の価値が小さくなり第2財の価値が大きくなっていると見ることもできる。
このように、一方の財の消費量を増やしていくと限界代替率が低下することを、限界代替率逓減の法則という。
無差別曲線の極端な例 完全代替財と完全補完財
無差別曲線の形状は、2つの財がどのような割合で代替できるかを反映している。2つの財が互いに代替されやすければ、無差別曲線は直線に近い形状になる。逆に代替が難しければ、原点に向かって大きな凸形状になる。この2つの極端な例が完全代替財と完全補完財である。
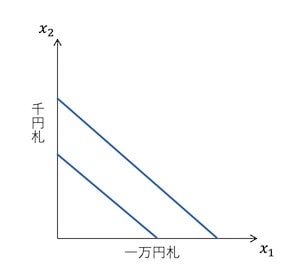
完全代替財
一万円札1枚と千円札10枚を比較すると価値は同じである。「千円札10枚はかさばるから嫌だ」などの理由は除いて価値だけを考えれば、限界代替率は常に一定であるため無差別曲線は右下がりの直線になる。このように、消費者にとって2つの財が完全に同じ財とみなされるものを完全代替財という。
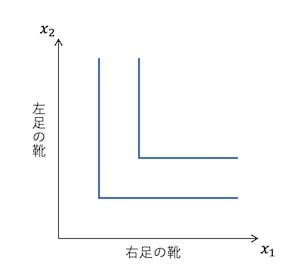
完全補完財
靴は右足と左足で形状が違う。右足用の靴をたくさん持っていても左足用の靴を1つしか持っていなければ、靴を1足しか持っていないのと同じ効用しか得られない。このような2つの財がそろって初めて効用が得られるような場合、無差別曲線はL字型になり、このような財を完全補完財という。