長期の生産関数

生産要素が労働 $L$ と資本 $K$ の2つの場合、生産関数は $y = F (L, K)$ と書ける。

もし生産に必要な要素が労働と資本だけならば、この2つの生産要素の量を自由に調整できるため、これは長期の生産関数であるといえる。

規模に関する収穫

すべての生産要素の投入量を $n$ 倍（ $n > 1$ ）したときに生産量がどう変化するのかは、以下の3通りが考えられる。

規模に関して収穫逓増：生産量が $n$ 倍より大きくなる
規模に関して収穫一定：生産量がちょうど $n$ 倍になる
規模に関して収穫逓減：生産量が $n$ 倍より小さくなる

通常は生産要素を $n$ 倍すれば生産量も $n$ 倍になるため収穫一定である。ただし、規模を拡大すると資本を安く購入できコストを抑えられたり、もっと効率的な生産方法が利用できる場合もあるため、このときは収穫逓増となる。

完全競争（投入量や生産量を変えても価格や賃金が変化しないケース）において、すべての生産要素が含まれている場合は、収穫逓減になることはない。投入量を $n$ 倍したのに生産量が $n$ 倍よりも小さくなるということは、他の隠れた生産要素が存在するということである。

完全競争ではない現実的な場面において、一般的には、ある一定水準までは規模に関して収穫逓増であるが、それ以降は収穫逓減であると考えられている。

等量曲線と技術的限界代替率

生産要素が２つの場合、同じ生産量を達成する生産要素の組み合わせは複数ある。横軸に労働 $L$ 、縦軸に資本 $K$ として、同じ生産量を達成できる点の集合をグラフにすると以下のようになり、この線は等量曲線と呼ばれる。

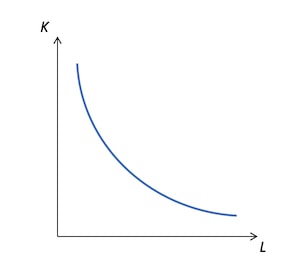
これは、資本を減らして労働を増やす（あるいは資本を増やして労働を減らす）ことで、これらを変化させる前と同じ生産量を達成できることを示している。つまり、生産要素間で代替できるわけである。

これは、消費者が2つの財の組み合わせで一定の効用を達成するための点の集合である無差別曲線と形式的には同じ概念である。つまり、一方の生産要素を限界的に1単位変化させたとき、もう一方の生産要素をどれだけ変化させれば同じ生産量を維持できるかを限界代替率とすることができる。無差別曲線の限界代替率と区別するために、技術的限界代替率と呼ぶこともある。無差別曲線の限界代替率と同じように「MRS」（Marginal Rate of Substitution）と表記され、労働 $L$ に対する資本 $K$ の限界代替率という場合には「MRS_LK」と表記される。

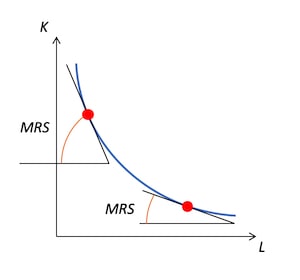
図を見ても分かる通り、等量曲線は原点に向かって凸の形をしているため、労働の投入量を増やしていくと限界代替率は低下していく。これは、技術的限界代替率逓減の法則と呼ばれる。

数式による表現

労働 $L$ 、資本 $K$ 、生産物 $y$ 、生産関数 $y = F (L, K)$ とし、「限界効用」のページと同様に考えていくと、生産要素を限界的に1単位変化させたときの生産量の変化 $d y$ は、

d y = \frac{\partial F}{\partial L} d L + \frac{\partial F}{\partial K} d K

と書ける。等量曲線は生産量が一定になる点の集まりなので、

0 = \frac{\partial F}{\partial L} d L + \frac{\partial F}{\partial K} d K

となる。

これを変形すると

\frac{d K}{d L} = - \frac{\partial F / \partial L}{\partial F / \partial K}

となる。

左辺は等量曲線の傾きであり、符号がマイナスになるのでプラスに変えたものが技術的限界代替率になる。右辺の分母と分子はそれぞれの生産要素での限界生産性であり、その比になっている。

参考書籍（PR）