パレート効率性
ここでは2人の消費者が2つの財を交換する規模の小さなモデルを用いる。このような、生産する企業のない消費者の交換だけのモデルは純粋交換経済と呼ばれる。
エッジワースのボックス・ダイアグラム
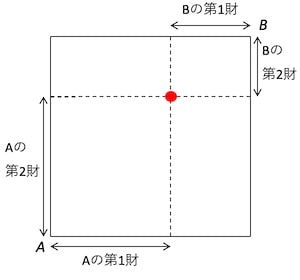
上図は、横軸に第1財、縦軸に第2財になっているが、左下が消費者Aの原点で右上が消費者Bの原点になっている。これは、消費者2人のそれぞれの財の配分を表している。この図に消費者2人の無差別曲線を描くと、下図のようになる。
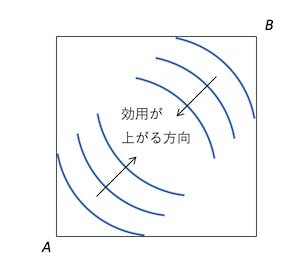
これは「エッジワース・ボックス」あるいは「エッジワースのボックス・ダイアグラム」と呼ばれる。
パレート改善とパレート効率的
下図のように、エッジワース・ボックス内で消費者2人の無差別曲線が交わる場合を考えていく。
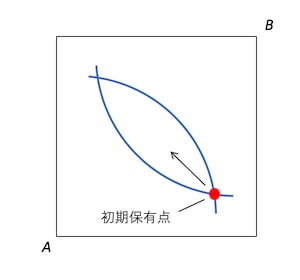
初期保有点は、2人の消費者が2つの財を保有する割合を示している。
2つの無差別曲線に囲まれた範囲というは初期保有点と比較すると、2人の消費者どちらの効用も下げることがない範囲である。無差別曲線上を除けば、両方の効用を上げることができる範囲とも言える。このように、誰の効用も下げることなく、少なくとも誰か1人の効用を上げることはパレート改善と呼ばれる。
パレート改善が進んでいくと、最終的に2つの無差別曲線は以下の図のようになる。
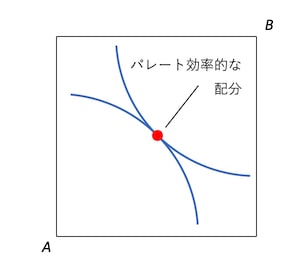
2つの無差別曲線が接している点が保有点になると、これ以上両者の効用を下げない資源配分が存在しなくなる、つまりパレート改善ができないことになる。このような状態はパレート効率的と呼ばれる。
パレート効率性の条件
無差別曲線の接線の傾きというのは、2つの財の限界代替率である。2つの無差別曲線の接点では、それぞれの接線の傾きが一致する、つまり限界代替率が同じになるということである。
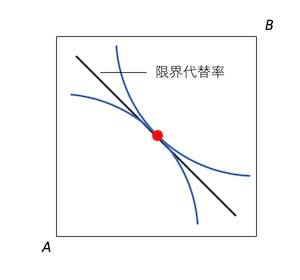
このことから、パレート効率的な資源配分の条件は、
契約曲線
エッジワース・ボックスで表現される無差別曲線の接点であるパレート効率的な状態は複数ある。この無差別曲線の接点の集合は契約曲線と呼ばれる。
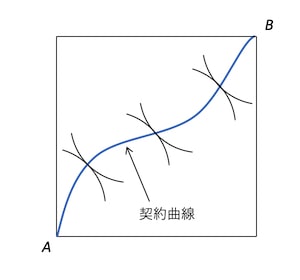
パレート効率的な状態は、必ずしも望ましい状態とは言えない。消費者AとBの資源配分に大きな偏りがあり不公平な配分であることもある。ただし、「誰の効用も下げることなく、少なくとも誰か1人の効用を上げることができる」というパレート改善を行っていった結果がパレート効率的な状態なわけだから、望ましい状態はパレート効率的な状態になっていることは明らかである。つまり、パレート効率的な状態は、望ましい状態の必要条件ではあるが十分条件ではないということである。