長期の利潤最大化

生産要素が労働と資本の2つで、完全競争の場合の利潤最大化を見ていく。

利潤は売上から費用を差し引いたもので、売上は生産物の価格 $p$ と生産量 $y$ の積となる。費用は、労働 $L$ と賃金 $w$ の積と、資本 $K$ と資本の価格 $r$ の積となる。生産関数は $y = F (L, K)$ となり、利潤を $π$ とすると、

π = p F (L, K) - w L - r K

と書ける。

生産物の価格 $p$ 、賃金 $w$ 、資本価格 $r$ は固定なので、労働 $L$ と資本 $K$ で利潤が最大になる組み合わせを見ていくことになる。

費用最小化

横軸を労働 $L$ 、縦軸を資本 $K$ とすると、生産量が最大になる組み合わせの等量曲線を描ける。この組み合わせの中で利潤が最も大きくなるのは、費用が最も小さくなる組み合わせである。

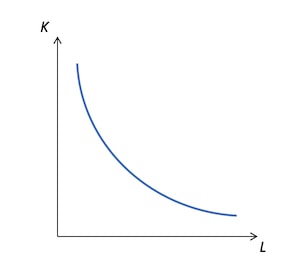
費用を $TC$ とすると、 $TC = w L - r K$ となり、これを変形すると、

K = - \frac{w}{r} L + \frac{TC}{r}

という直線の式が得られる。これは等費用線と呼ばれ、その傾きは生産要素の価格比

w

r

になる。そして、等量曲線と等費用線が接する点が費用最小点となる。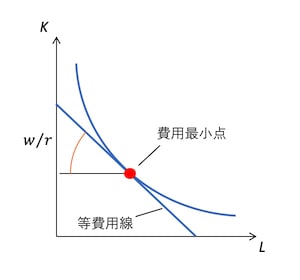

等量曲線との接点が費用最小点になるということは、技術的限界代替率と同じになるということである。また、「長期の生産関数」のページでも見たように、技術的限界代替率は限界生産性の比でもある。つまり、限界生産性の比と生産要素の価格比が同じとなる、

\frac{\partial F / \partial L}{\partial F / \partial K} = \frac{w}{r}

も成り立つ。

ミクロ経済学では、生産関数を凹関数と考えることが多い。

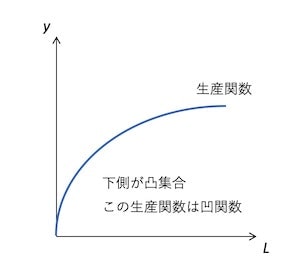
生産関数が凹関数の場合、

π = p F (L, K) - w L - r K

は凹関数になる。これは、

p F (L, K)

が凹関数となり、

- w L - r K

が1次式となるからである。

縦軸に利潤、横軸に労働と資本の3軸のグラフを描くと、利潤のグラフは上に向かって凸の形になる。つまり、頂点が利潤最大点となるが、この点では接線の傾きがゼロになるということでもある。

利潤をそれぞれの生産要素で微分し、ゼロになる点が利潤最大点となるわけだから、

\frac{\partial π}{\partial L} = 0

\frac{\partial π}{\partial K} = 0

が、利潤最大化条件となる。ただし、生産関数が凹関数の場合は必要十分条件であるが、凹関数でない場合は必要条件ではあるが十分条件ではない。

また、 $π = p F (L, K) - w L - r K$ から、

\frac{\partial π}{\partial L} = p \frac{\partial F}{\partial L} - w = 0

\frac{\partial π}{\partial K} = p \frac{\partial F}{\partial K} - r = 0

となり、整理すると、

p \frac{\partial F}{\partial L} = w

p \frac{\partial K}{\partial L} = r

となる。左辺は限界生産物の価値であり、右辺は生産要素の価格である。生産要素を限界的に1単位増やしたときに、限界生産物の価値の増加とコストの増加が一致するところが、利潤最大点となる。

この上の式を下の式で割ると、

\frac{\partial F / \partial L}{\partial F / \partial K} = \frac{w}{r}

という式ができる。これは、限界生産性の比と生産要素の価格比であり、上で見た費用最小化の条件でもある。

参考書籍（PR）