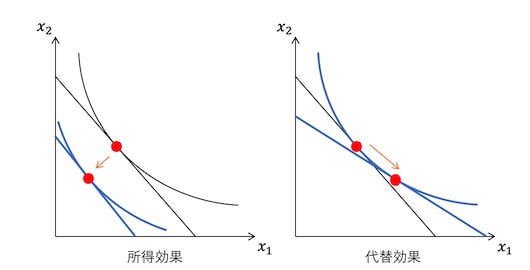
所得効果と代替効果

財の価格の変化による消費への影響は、所得効果と代替効果に分けられる。

ある財の価格が上がると、同じ金額でその財を消費できる量が減ることを意味している。つまり、財の価格が上がると、所得が変わらなくても実質的には所得が目減りしていることになるため、その財の消費量は減少し、他の財の消費量も減少するかもしれない。このように、ある財の価格が変化したときに、実質的な所得が変化することによって財の消費量に影響を与える効果を所得効果という。

一方で、ある財の価格が上がったときに、その財の代わりになる代替財があると消費の乗り換えが起こる。このような、乗り換えによって消費量に影響を与える効果を代替効果という。

無差別曲線と予算制約線を用いて表すと、所得効果は無差別曲線の移動によって生じる消費の変化であり、代替効果は同一の無差別曲線上で予算制約線の傾き（限界代替率）が異なることによって生じる消費の変化として捉えることができる。

スルツキー分解

所得 $I$ 、価格 $p$ 、効用 $u$ 、補償需要 $h$ 、消費量 $x$ とした場合の効用最大化問題と支出最小化問題の双対性の関係式は

h (p, u) = x (p, I)

であった。

このとき、所得 $I$ は、価格 $p$ で効用 $u$ を達成するための最低限必要な金額である。つまり、所得 $I$ は、支出関数 $e (p, u)$ で表せるので、これを双対性の関係式に代入すると、

h (p, u) = x (p, e (p, u))

となる。第

i

財についてみれば、

h_{i} (p, u) = x_{i} (p, e (p, u))

である。

これを $p_{i}$ で微分すると、

\frac{\partial h_{i}}{\partial p_{i}} = \frac{\partial x_{i}}{\partial p_{i}} + \frac{\partial x_{i}}{\partial e} \frac{\partial e}{\partial p_{i}}

となる。

$x = x (p, I)$ なので、双対性の関係式から

h (p, u) = x

であることがわかる。

これをシェファードの補題 $\frac{\partial e (p, u)}{\partial p_{i}} = h_{i} (p, u)$ に代入すると、

\frac{\partial e (p, u)}{\partial p_{i}} = x_{i}

となる。

これを先程の $p_{i}$ で微分した式の最後の項に代入し、移行すると、

\frac{\partial x_{i}}{\partial p_{i}} = \frac{\partial h_{i}}{\partial p_{i}} - \frac{\partial x_{i}}{\partial e} x_{i}

となる。これをスルツキー方程式あるいはスルツキー分解式という。

所得 $I = e (p, u)$ なので、

\frac{\partial x_{i}}{\partial p_{i}} = \frac{\partial h_{i}}{\partial p_{i}} - \frac{\partial x_{i}}{\partial I} x_{i}

としたほうがわかりやすいかもしれない。

この式の左辺は、価格の変化による需要の変化を表している。

右辺の第1項は、価格の変化による補償需要の変化であり代替効果を示している。「補償需要関数と支出関数」のページでも見たが、補償需要は代替性や補完性の程度を表しており、この式の場合は自己代替効果なので、価格が上昇した場合には必ずゼロかマイナスになる、つまり他の財への代替が起こることを意味する。

右辺の第2項は所得効果になるが、このままではわかりづらいので、価格変化 $Δ p_{i}$ によって引き起こされた需要の変化 $Δ x_{i}$ を見ると、

Δ x_{i} \approx \frac{\partial h_{i}}{\partial p_{i}} Δ p_{i} - \frac{\partial x_{i}}{\partial I} x_{i} Δ p_{i}

となり、

x_{i} Δ p_{i}

は、効用を一定に保つための所得変化を示している。これは、

i

財の価格が上がると所得が目減りすることを表している。

この符号込みの所得効果（ $- \frac{\partial x_{i}}{\partial I} x_{i}$ ）は、財の価格が上がった場合は、正常財ならマイナスに、劣等財ならプラスになる。

ちなみに、上のスルツキー方程式は、 $i$ 財の価格の変化が $i$ 財の消費量（需要）に与える影響を表しているが、 $p_{i}$ ではなく $p_{j}$ で微分すれば、 $p_{j}$ の価格の変化が $i$ 財の消費に与える影響を表せる。

参考書籍（PR）